diagramavenn
web west
grafica de barras
lineas de tiempo
flujogramas
cuadros comparativos
cuadros sinoptico
viernes, 29 de agosto de 2014
EJEMOLOS DE TIPOS DE REPRECENTACIONES GRAFICAS
Ejemplos de tipos de representaciones gráficas
Histogramas: Se agrupan los datos en clases, y se cuenta cuántas observaciones (frecuencia absoluta) hay en cada una de ellas. En algunas variables (variables cualitativas) las clases están definidas de modo natural, p.e sexo con dos clases: mujer, varón o grupo sanguíneo con cuatro: A, B, AB, O. En las variables cuantitativas, las clases hay que definirlas explícitamente (intervalos de clase).
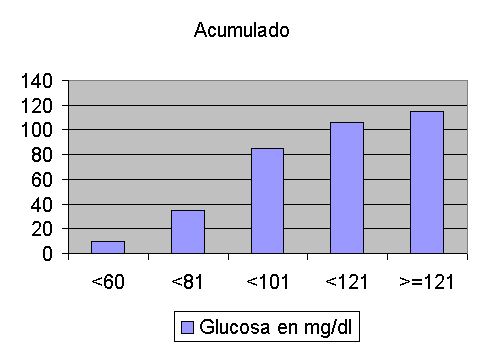 A veces es más útil representar las frecuencias acumuladas.
A veces es más útil representar las frecuencias acumuladas.
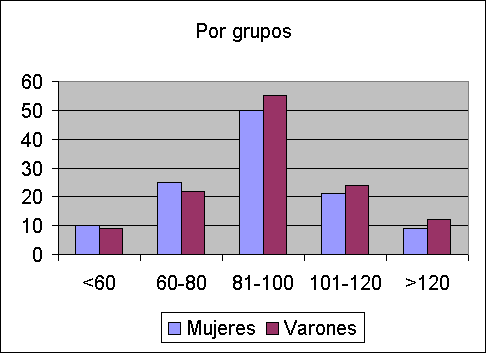
O representar simultáneamente los histogramas de una variable en dos situaciones distintas.
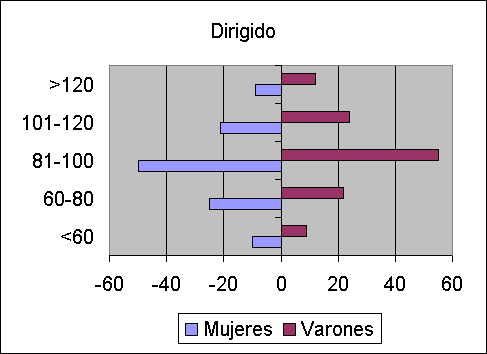
Otra forma muy frecuente, de representar dos histogramas de la misma variable en dos situaciones distintas.
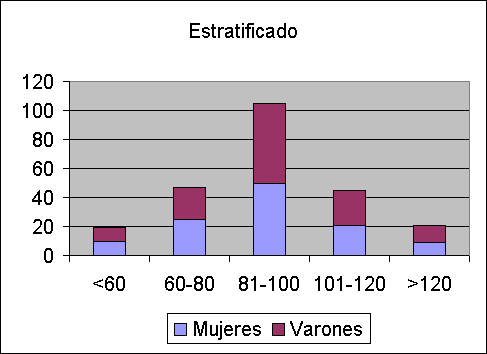
otra mas
Se representan los intervalos de clase en el eje de abcisas (eje horizontal) y las frecuencias, absolutas o relativas, en el de ordenadas (eje vertical).


O representar simultáneamente los histogramas de una variable en dos situaciones distintas.

Otra forma muy frecuente, de representar dos histogramas de la misma variable en dos situaciones distintas.

otra mas

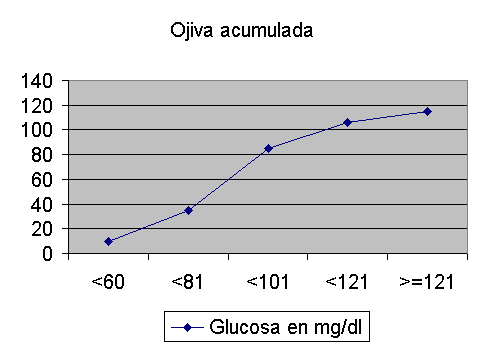
En las variables cuantitativas o en las cualitativas ordinales se pueden representar polígonos de frecuencia en lugar de histogramas, cuando se representa la frecuencia acumulativa, se denomina ojiva. |
viernes, 15 de agosto de 2014
Ejemplos de tipos de representaciones gráficas
Histogramas: Se agrupan los datos en clases, y se cuenta cuántas observaciones (frecuencia absoluta) hay en cada una de ellas. En algunas variables (variables cualitativas) las clases están definidas de modo natural, p.e sexo con dos clases: mujer, varón o grupo sanguíneo con cuatro: A, B, AB, O. En las variables cuantitativas, las clases hay que definirlas explícitamente (intervalos de clase).
Se representan los intervalos de clase en el eje de abcisas (eje horizontal) y las frecuencias, absolutas o relativas, en el de ordenadas (eje vertical).A veces es más útil representar las frecuencias acumuladas.
O representar simultáneamente los histogramas de una variable en dos situaciones distintas.Otra forma muy frecuente, de representar dos histogramas de la misma variable en dos situaciones distintas.
En las variables cuantitativas o en las cualitativas ordinales se pueden representar polígonos de frecuencia en lugar de histogramas, cuando se representa la frecuencia acumulativa, se denomina ojiva.
viernes, 1 de agosto de 2014
todo sobre
Un histograma es una representación gráfica de una variable en forma de barras, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados. En el eje vertical se representan las frecuencias, y en el eje horizontal los valores de las variables, normalmente señalando las marcas de clase, es decir, la mitad del intervalo en el que están agrupados los datos.
Se utiliza cuando se estudia una variable continua, como franjas de edades o altura de la muestra, y, por comodidad, sus valores se agrupan en clases, es decir, valores continuos. En los casos en los que los datos son cualitativos (no-numéricos), como sexto grado de acuerdo o nivel de estudios, es preferible un diagrama de sectores.
Los histogramas son más frecuentes en ciencias sociales, humanas y económicas que en ciencias naturales y exactas. Y permite la comparación de los resultados de un proceso.
Los Histogramas, son utilizados como una herramienta que ayuda en la toma de decisión para la resolución de problemas, mediante el histograma se puede identificar las pautas de comportamiento del conjunto de los datos y extraer conclusiones, así los histogramas la cual nos permite:
*Realizar un análisis de distribución de datos.
*Comprobar el grado de cumplimiento de las especificaciones.
*Evaluar la eficacia de las soluciones.
Método de aplicación de los histogramas
Previo a la explicación de los pasos a seguir para elaborar un histograma, tenemos que conocer algunos conceptos previos como:
•Recorrido o rango (R): es el valor resultante de restar el valor máximo y el mínimo.
•Clase (k): es la dimensión de un intervalo de variabilidad de los datos.
•Frecuencia: número de elementos comprendidos en una determinada clase.
Los pasos a seguir son:
1.Recoger todos los datos (N) en una hoja de datos, en los histogramas se trabaja con datos, a menudo, con tiempos, pesos, tamaños…, y por lo tanto cuantos más datos obtengamos más exacto será el Histograma. El número total de valores se denominará “N”.
2.Obtener los valores máximo (Vmáx.) y mínimo (Vmín.).
3.Establecer el recorrido o rango (R) de la siguiente forma: R = Vmáx. – Vmín, como vemos en la fórmula, simplemente deberemos restar el valor máximo de los datos obtenidos del valor mínimo.
4.Determinar el número de clases (k) que queremos que exista, con este dato determinaremos las barras que queremos que aparezcan en el Histograma, facilitándonos cuantas clases o grupos tenenos.
5.Calcular la amplitud de cada clase de la siguiente manera: i = R / k.
6.Redondear, al valor entero superior, si el resultado no es exacto en términos de la unidad.
7.Establecer los valores de los límites de clase.
8.Construir una tabla de distribución de frecuencias y asignar los datos obtenidos a su clase correspondiente, al hacerlo podemos encontrarnos con el problema de que tengamos valores en el límite entre una clase y otra, y no sepamos a cuál de las dos clases asignarlo, en este caso se recomienda asignar estos datos a una de las dos clases, la inferior o la superior, pero siempre con el mismo criterio, para no desvirtuar el gráfico.
9.Construir los ejes del histograma, para construirlos seguiremos los siguientes criterios, en el eje horizontal se colocan los valores de las marcas de clase y sobre el eje vertical se colocan los valores de las frecuencias.
10.Trazar los rectángulos correspondientes, una vez se hayan determinado los intervalos y sepamos cuántas mediciones caen dentro de cada intervalo, deberemos poner los rectángulos en función de los ejes del histograma.
*Definición
Es un resumen gráfico de los valores producidos por las variaciones de una
determinada característica, representando la frecuencia con que se presentan
distintas categorías dentro de dicho conjunto.
Ejemplo: Días pasados hasta contestar una reclamación
*Características principales
A continuación se comentan una serie de características que ayudan a
comprender la naturaleza de la herramienta.
Síntesis
Permite resumir grandes cantidades de datos.
Análisis
Permite el análisis de los datos evidenciando esquemas de comportamiento y
pautas de variación que son difíciles de captar en una tabla numérica.
Capacidad de comunicación
Permite comunicar información de forma clara y sencilla sobre situaciones
complejas.
Suscribirse a:
Comentarios (Atom)
